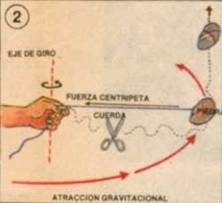
La Segunda Ley de Newton se
puede resumir como sigue: La aceleración de un objeto es directamente
proporcional a la fuerza neta que actúa sobre él, e inversamente
proporcional a su masa.
La dirección de la aceleración es la
misma de la fuerza aplicada.
A representa la
aceleración, m la masa y F la fuerza neta. Por fuerza
neta se entiende la suma vectorial de todas las fuerzas que actúan
sobre el cuerpo
Definición de Masa, Inercia
¿Qué es
la masa? Newton mismo usó el término masa como
sinónimo de cantidad de materia. Esta noción no es muy precisa. Con más
precisión podemos decir que la masa es una medida de la inercia
de un cuerpo. Mientras más masa tenga un cuerpo, es más difícil cambiar su
estado de movimiento. Es más difícil hacer que comience a moverse partiendo del
reposo, o detenerlo cuando se mueve, o hacer que se mueva hacia los lados saliiéndose de su trayectoria recta. Un camión tiene mucho más inercia que una
pelota de tenis que se mueva a la misma velocidad, siendo mucho más difícil
cambiar el estado de movimiento del camión.
Para cuantificar el concepto de masa
debe definirse un patrón. En unidades del Sistema Internacional (SI),
la unidad de masa es el kilogramo (kg). El patrón actual es
un cilindro de platino-iridio que se conserva en la Oficina Internacional
de Pesas y Medidas cerca de París, cuya masa, por definición, es
exactamente un kilogramo. En unidades CGS, la unidad de masa es
el gramo (g) y 1g = 10-3 kg. En el sistema
ingles, la unidad de masa se llama slug.
No debe confundirse
la masa con el peso. La masa es una propiedad de un
cuerpo, es una medida de su inercia o cantidad de materia.
El peso es una fuerza, la fuerza que latiera ejerce sobre
el cuerpo. Para aclarar la diferencia, supongamos que llevamos un objeto a la
Luna. Allí pesará la sexta parte de lo que pesaba en la Tierra, pero su masa
seguirá siendo la misma.
Aceleración, Fuerza
Neta
La Primera ley de
Newton afirma que en ausencia de fuerza neta sobre un
cuerpo, éste permanece en reposo, o si está en movimiento, continúa moviéndose
con velocidad constante (conservando su magnitud y dirección).
Pero, ¿qué sucede si una fuerza actúa sobre un cuerpo? La velocidad debe
cambiar, o sea, una fuerza neta origina una aceleración.
La relación entre aceleración y fuerza podemos
encontrarla en experiencias cotidianas. Pensemos que empujamos un carrito de
supermercado. La fuerza neta que se ejerce sobre el carrito es la fuerza que yo
aplico menos la fuerza de fricción en las ruedas. Si la fuerza neta es F, la aceleración
será a, si la fuerza es 2F, la aceleración será 2a, y así sucesivamente. Por
tanto, la aceleración de un cuerpo es directamente proporcional a la
fuerza neta aplicada. Pero la aceleración depende también de
la masa del objeto. Si mantengo la fuerza neta F y aumento la masa al
doble, la aceleración será a/2.
O sea, podemos afirmar
Se escoge la unidad de fuerza de tal
modo que la constante de proporcionalidad en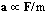 ,
sea 1, y así
,
sea 1, y así
a
= F/m
Notemos que mediante esta segunda
ley podemos dar una definición más precisa de fuerza, como una
acción capaz desacelerar un objeto.
Cuando la masa está
en kilogramos y la aceleración en metros por segundo al
cuadrado, la unidad de fuerza se llama Newton (N), 1 N = 1kgm/s2.
En el sistema ingles,
la unidad de fuerza es la libra. Se define como el peso (que es
una fuerza) de un cuerpo cuya masa es 0.45359237 kg en determinado lugar de la
Tierra en el que la aceleración de gravedad sea 32.1734 pies/s2.
Ejemplos
1.Al aplicar una
fuerza de 92N se acelera a razón de 12M/s2 ¿cual será su masa?
F=92N
a=12m/s2 m= 96Kg * m/s2/12m/s2= 8Kg
m=8Kg
2.Que fuerza se
ejerce sobre un cuerpo de 25Kg para que se acelere 12.5m/s2
m=25Kg
F=25kg * 12.5m/s2= 31.5N
a=12.5m/s2
3.Sobre un cuerpo de 15Kg actúa una fuerza de 32N ¿Que aceleración
tendrá?
m=15Kg a=32Kg*m/s2/15Kg
f=32N a=2.1333m/s2
4.Que fuerza se
ejerce sobre un cuerpo de 30Kg para que se acelere 15m/s2
m=30Kg f=30Kg*15m/s2
a=15m/s2 f=450N
5.Sobre un cuerpo de
2Kg se ejerce una fuerza de 10N ¿cual será su aceleración?
m=2Kg a=10Kg*m/s2/2Kg